Trigonometry formulas list: trigonometry, is a major part of quantitative aptitude, which students find quite difficult. Trigonometry is a major branch of mathematics that deals with the angle and length of a triangle. There are a total of 6 trigonometric functions named Sin, Cos, Tan, Sec, Cosec, and Cot. Through these trigonometric ratios, length and angle are known. All the formulas, tricks, and questions of trigonometry are related to these 6 functions.
What is trigonometry?
Trigonometry is that branch of mathematics in which triangles and polygons formed from triangles are studied. Trigonometry literally means ‘measurement of a triangle’ (from Greek trigōnon, “triangle” and metron, “measure”). The most important in trigonometry is the study of right-angled triangles. The main basis of studying the lengths of the sides of triangles and polygons and the angles between two sides is that the ratio of any two sides (base, length, and hypotenuse) of a right triangle depends on the value of the angles of that triangle. Trigonometry is closely related to the famous Buddhist theorem (Pythagoras theorem) of geometry.
trigonometry Questions related are asked in various competitive exams like SSC, Railways, etc. In this post, we are providing you useful trigonometry notes or Formulas for Competitive exams. This will help you to remember the basic formula of trigonometry. Important trigonometric ratios (Trigonometry Ratios-Sine, Cosine, Tangent):
For a stronghold on the basic concept of trigonometry, you must know all the important trigonometric ratios and their identities.
Trigonometry Ratios:
To study the different trigonometric ratio functions, we will take a right-angled triangle. Suppose ABC is a right-angled triangle and B = 90 °.

Trigonometric Ratios
sinθ = Perpendicular/ Hypotenuse
cosθ = Base/ Hypotenuse
tanθ = Perpendicular/ Base
secθ = Hypotenuse/ Base
cosecθ = Hypotenuse/ Perpendicular
cotθ = Base/ Perpendicular
Trigonometric Ratios in Different Quadrants
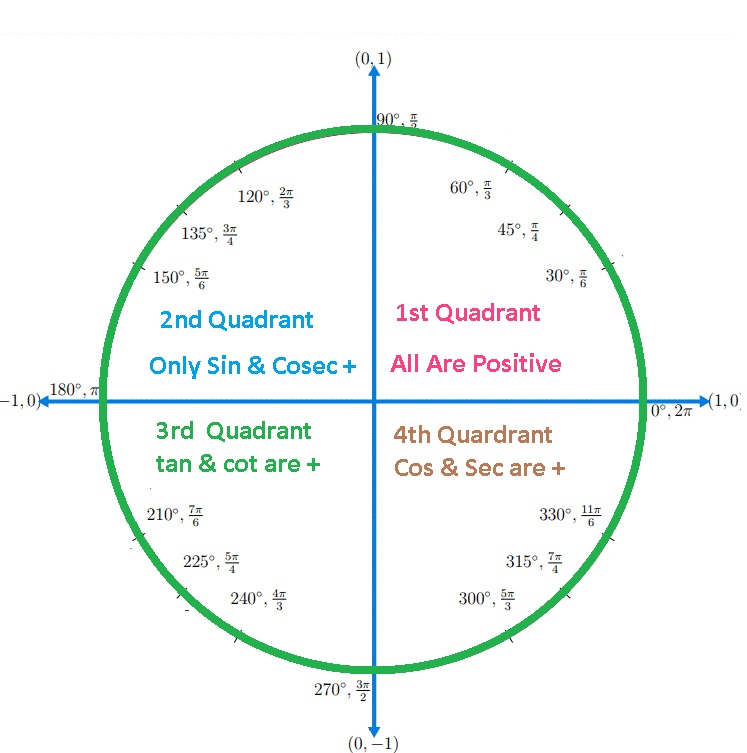
- Sin (90– A) = Cos A
- Cos (90– A) = Sin A
- Sin (90+ A) = Cos A
- Cos (90+ A) = – Sin A
- Sin (270 – A) = – Cos A
- Cos (270 – A) = – Sin A
- Sin (270 + A) = – Cos A
- Cos (270 + A) = Sin A
- Sin (360 – A) = Sin A
- Cos (360 – A) = – Cos A
- Sin (360 + A) = – Sin A
- Cos (360 + A) = – Cos A
- Sin (360 – A) = – Sin A
- Cos (360 – A) = Cos A
- Sin (360 + A) = Sin A
- Cos (360 + A) = Cos A
Important Conversions in Trigonometry
(90° + θ)
(90° – θ)
(270° + θ)
(270° – θ)
Below Important Conversation are given for 1st and 3rd Quadrant
sin θ <====> cos θ
tan θ <=====> cot θ
Cosec θ <=====> sec θ
These conversation is not applicable for the Angle 0° or 360° and 180°.

Division of Quadrants
| (90° – θ) | 1st Quadrant |
| (90° + θ) and (180° – θ) | 2nd Quadrant |
| (180° + θ) and (270° – θ) | 3rd Quadrant |
| (270° + θ), (360° – θ) and (- θ) | 4th Quadrant |
Trigonometry Table
| Degrees OR Angle θ = | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Trigonometric Ratio Or Radians | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Cosec θ | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |